VIDEOS RELACIONADOS

VÍDEOS CIRCUITOS COMBINACIONALES 

VÍDEO DE CIRCUITOS SECUENCIALES

CIRCUITOS SECUENCIALES

INTRODUCCIÓN

Los sistemas digitales que introducen la dependencia temporal son conocidos como sistemas secuenciales. Una definición más rigurosa de sistema secuencial puede ser la siguiente: Un circuito de conmutación secuencial se define como un circuito bivaluado en el cual, la salida en cualquier instante depende de las entradas en dicho instante y de la historia pasada (o secuencia) de entradas.

CARACTERÍSTICAS

• Poseen uno o más caminos de re-alimentación, es decir, una o más señales internas o de salida se vuelven a introducir como señales de entradas. Gracias a esta característica se garantiza la dependencia de la operación con la secuencia anterior. 

• Como es lógico, existe una dependencia explícita del tiempo. Esta dependencia se produce en los lazos de re-alimentación antes mencionados. En estos lazos es necesario distinguir entre las salidas y las entradas re-alimentadas.

ELEMENTOS

• Elementos de retraso, ya sean explícitos o implícitos debido al retraso de la lógica combinacional. Este retraso es fijo e independiente de cualquier señal.

 • Elementos de memoria, que son dispositivos que almacena el valor de la entrada en un instante determinado por una señal externa y lo mantiene hasta que dicha señal ordene el almacenamiento de un nuevo valor. La diferencia de comportamiento entre ambos elementos radica en que la salida del elemento de retraso es una copia de la señal de entrada; mientras que el elemento de memoria copia determinados instantes de la entrada (determinados por una señal externa), y no la señal completa, el resto del tiempo la salida no cambia de valor

Circuitos Lógicos Secuenciales

Los bloques básicos para construirlos son los circuitos flip-flops.  Los circuitos lógicos secuenciales son extremadamente importantes debido a su característica de memoria.

Los flip-flops también se denominan "cerrojos", "multivibradores biestables" o "binarios".  Los flip-flops pueden construirse a partir de puertas lógicas, como, por ejemplo, puertas NAND, o comprarse en forma de circuitos integrados.  Los flip-flops se interceptaran para formar circuitos lógicos secuenciales que almacenen datos, generen tiempos, cuenten y sigan secuencias.

Funcionalidad

El circuito secuencial debe ser capaz de mantener su estado durante algún tiempo, para ello se hace necesario el uso de dispositivos de memoria. Los dispositivos de memoria utilizados en circuitos secuenciales pueden ser tan sencillos como un simple retardador (inclusive, se puede usar el retardo natural asociado a las compuertas lógicas) o tan complejos como un circuito completo de memoria denominado multivibrador biestable o Flip Flop

FLIP-FLOP D

Tiene solamente una entrada de datos (D) y una entrada de reloj (CK).  El flip-flop D, con frecuencia, se denomina flip-flop de retardo (y de datos).  Este nombre describe con precisión la operación que realiza.  Cualquier que sea el dato en la entrada (D), éste aparece en la salida normal retardado un pulso de reloj.  El dato es transferido a la salida durante la transición del nivel BAJO al ALTO del pulso de reloj.

Otros nombres usados para este tipo de circuitos son: MultiVibradores, Basculas, Bies-tables

Los Flip-Flops son las unidades básicas de todos los sistemas secuenciales. Existen cuatro tipos: el RS, el JK, el T y el D. Y los últimos tres se implementan del primero.


Son capaces de permanecer en un estado determinado durante un tiempo indefinido. Esta característica es amplia mente utilizada para memorizar información.



El Flip Flop SR (Set/ Reset), abreviadamente FF-SR

El FF-SR es un dispositivo con dos entradas (Set y Reset) y una variable de estado o salida (Q) capaz de guardar un bit de información y funciona como sigue:

Si la entrada Set pasa a 1 la salida Q pasa 1
Si la entrada Reset pasa a 1 la salida Q pasa a 0
Si ni Set ni Reset cambian la salida Q no cambia
Set y Reset no pueden cambiar simultáneamente.






FLIP-FLOP JK

Este dispositivo puede considerarse como el flip-flop universal; los demás tipos pueden construirse a partir de él.





Tabla de Funcionamiento

La tabla de funcionamiento de este circuito es parecida a la de un combinacional pero en la cual se ha introducido la información "tiempo" que en el caso de circuitos secuenciales se vuelve esencial.

Entradas en tn Salida en tn+1
S R Q+

0 0 Q0
0 1 0
1 0 1
1 1 no valida

En donde se ha utilizado la siguiente notación:

tn = instante en el cual se aplican las entradas.

tn+1 = instante siguiente, cuando el circuito proporciona su salid

Q0 = salida Q en el instante tn

Q+ = salida en el instante tn+1

Aplicaciones de los Flip-Flop

Todos estos tipos de Flip-Flops se emplean para construir módulos funcionales que realizan tareas de mas alto nivel, algunas de las cuales describir a continuación.

Contadores

Permiten llevar la cuenta del número de veces que se repite un suceso. Para ello memorizan la cuenta actual y la incrementan cada vez que el evento vuelve a ocurrir. Como elemento de memoria se usa algún tipo de Flip-Flop, tantos como sea precisos para memorizar la cantidad máxima que este previsto contar.





Clasificación de los Sistemas Secuenciales

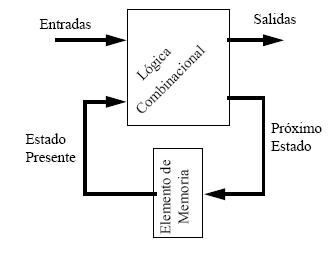
Uno de los primeros problemas de los circuitos secuenciales era determinar el momento en el que el próximo estado debía pasar a estado presente, sin capturar situaciones no deseadas como pueden ser los azares. Este problema es lo que se conoce como sincronizar, cuyas soluciones dieron lugar a una de la principales clasificaciones de los sistemas secuenciales. Así podemos dividir los sistemas en dos categorías: Lógica Combinacional Elemento de Memoria Entradas Salidas Próximo Estado Presente Estado Figura 1.3.- Modelo clásico de un sistema secuencial.

• Sistemas asíncronos.- La sincronización depende exclusivamente de los retrasos de la lógica combinacional, sin necesidad de ninguna señal externa al sistema.

• Sistemas síncronos.- La sincronización depende exclusivamente de una señal externa al sistema, conocida generalmente como señal de reloj. Esta señal de reloj controlará el comportamiento de los elementos de memoria

Las operaciones de un sistema asíncrono tienen efecto, es decir, se almacena el próximo estado, en intervalos temporales diferentes. Por lo tanto, su velocidad de operación será distinta para cada secuencia de entradas. De esta forma se toma como el parámetro de la velocidad de operación el valor medio de todas las velocidades. Así, la operación de un sistema asíncrono se denomina operación del caso medio. 

En cambio, las operaciones de un sistema síncrono tienen efecto en el mismo intervalo temporal, el dictaminado por el periodo de la señal de reloj. Por lo tanto, su velocidad de operación será siempre la misma para todas las secuencias de entrada. Esta velocidad debe ser tal que todas las operaciones tengan el tiempo necesario para poder llevarse a cabo. Así, la velocidad de un sistema síncrono (y por tanto la frecuencia de la señal de reloj asociada) debe estar limitada por la operación más lenta. A este tipo de operaciones se le suele denominar operación del caso peor.

Ejemplo de diseño de un contador

Se desea un contador que solo pueda contar 0, 1, 2, 3 y 4. A un contador as se le denomina contador módulo 5 pues, no importa cuantas veces ocurra el suceso el conteo ser 0, 1, 2, 3 4, lo cual corresponde al resto de dividir el conteo real por 5 (por ejemplo, si el suceso se ha repetido 7 veces, el contador haber entregado los conteos 1, 2, 3, 4, 0, 1, 2 siendo el ultimo valor entregado 2, que es el resto de dividir 7 por 5)

Est claro que los estados diferentes que podr tener el sistema secuencial buscado sern cinco. Adems, las transiciones entre estados estn tambin muy claras: del estado 0 slo se puede pasar al 1, del 1 al 2, del 2 al 3, del 3 al 4, y por ltimo de 4 al 0. No habiendo posibilidad de otras transiciones entre estados. La nica entrada del sistema es la seal a contar E.

Con esto en mente podemos construir la tabla siguiente:

Entrada ESuceso a contar	Estado Actual			Estado Siguiente			Flip Flop 2		Flip Flop 1		Flip Flop 0
	Q2	Q1	Q0	Q2+	Q1+	Qo+	J2	K2	J1	K1	J0	K0
pasa de 0 a 1	0	0	0	0	0	1	0	X	0	X	1	X
pasa de 0 a 1	0	0	1	0	1	0	0	X	1	X	X	1
pasa de 0 a 1	0	1	0	0	1	1	0	X	X	0	1	X
pasa de 0 a 1	0	1	1	1	0	0	1	X	X	1	X	1
pasa de 0 a 1	1	0	0	0	0	0	X	1	0	X	0	X

A partir de esta tabla se pueden encontrar fcilmente las relaciones entre el estado actual o de partida, y las entradas de los Flip Flop:

Representación de los sistemas secuenciales.

 De igual forma que existe una representación de los sistemas combinacionales (mediante tablas de combinaciones), los sistemas secuenciales también tienen sus formas de representación. Éstas son algo más complejas, debido a la dependencia temporal. Así, podemos encontrar las siguientes formas equivalentes.

 • Diagrama de estados, es un grafo orientado en el que cada nudo es un estado y cada transición indica el cambio, tanto de estado como de salida, respecto a un cambio en alguna de las señales de entradas.

 • Tablas de estado y de salida, es una representación tabular del grafo anterior. Las entradas se representan como columnas, y los estados presentes como filas; y en el interior de cada celda, se indica el próximo estado y el valor que tomará la salida cuando sufra la transición.

Los computadores son implementaciones de lógica Booleana:

. • Las funciones Booleanas se describen completamente por medio de tablas de verdad.

 • Las compuertas lógicas son pequeños circuitos eléctricos que implementan operadores lógicos. 

• Los computadores consisten de circuitos lógicos combinacionales y secuenciales

 • Los circuitos combinacionales producen salidas inmediatamente después de que sus entradas cambian.

 • Los circuitos secuenciales requieren de las señal de reloj para producir cambios en las salidas 

• Los circuitos secuenciales básicos son los flip flops. 

• El comportamiento de los circuitos secuenciales puede ser expresado utilizando tablas de comportamiento.

En todo CIRCUITO SECUENCIAL nos encontraremos con:

a) Un conjunto finito, n, de variables de entrada (X1, X2,..., Xn).

b) Un conjunto finito, m, de estados internos, de aquí que los estados secuenciales también sean denominados AUTÓMATAS FINITOS. Estos estados proporcionarán m variables internas (Y1,Y2,..., Ym).

c) Un conjunto finito, p, de funciones de salida (Z1, Z2,..., Zp).

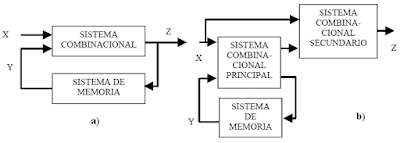
Dependiendo de como se obtengan las funciones de salida, Z, los sistemas secuenciales pueden tener dos estructuras como las que se observan en la siguiente figura, denominadas:

a) Máquina de Moore.

b) Máquina de Mealy.

SIMBOLOGIA

FIGURA.1

FIGURA.2

CONTADOR

EJERCICIOS COMBINACIONALES

IMPLEMENTACIÓN  DE  CIRCUITOS  COMBINACIONALES

CON PUERTAS LÓGICAS.

-Representación de funciones: mapas de Karnaugh de hasta 5 variables.

  El Mapa de Karnaugh es una representación gráfica de una función booleana. Los minitérminos
adjuntos (vecinos) sólo se diferencian en una variable. Se consideran vecinos también los extremos. La
numeración de las filas y columnas es un código GRAY.

1)  Para dos variables:

                     B  0     1      A B │ F
                   A ┌─────┬─────┐      ────┼──
                   0 │  0  │  1  │      0 0 │ 0    lugar 0
                     ├─────┼─────┤      0 1 │ 1  lugar 1
                   1 │  1  │  1  │      1 0 │ 1   lugar 2
                     └─────┴─────┘      1 1 │ 1  lugar 3

2)  Para tres variables:

                    BC 00    01    11    10    A B C │ F
                   A ┌─────┬─────┬─────┬─────┐  ──────┼──
                   0 │  1  │  0  │  0  │  1  │  0 0 0 │ 1  lugar 0
                     ├─────┼─────┼─────┼─────┤  0 0 1 │ 0  lugar 1
                   1 │  1  │  0  │  1  │  0  │  0 1 0 │ 1  lugar 2
                     └─────┴─────┴─────┴─────┘  0 1 1 │ 0  lugar 3
                1 0 0 │ 1  lugar 4
1 0 1 │ 0  lugar 5
1 1 0 │ 0  lugar 6
                 1 1 1 │ 1  lugar 7

3)  Para cuatro variables:

              CD 00    01    11    10    A B C D │ F
             AB┌─────┬─────┬─────┬─────┐    ────────┼──
             00│  1  │  0  │  0  │  1  │    0 0 0 0 │ 1 lugar 0
               ├─────┼─────┼─────┼─────┤    0 0 0 1 │ 0 lugar 1
             01│  1  │  1  │  1  │  0  │    0 0 1 0 │ 1 lugar 2
               ├─────┼─────┼─────┼─────┤    0 0 1 1 │ 0 lugar 3
             11│  0  │  1  │  1  │  1  │    0 1 0 0 │ 1 lugar 4
               ├─────┼─────┼─────┼─────┤    0 1 0 1 │ 1 lugar 5
             10│  1  │  1  │  0  │  1  │    0 1 1 0 │ 0 lugar 6
               └─────┴─────┴─────┴─────┘    0 1 1 1 │ 1 lugar 7
1 0 0 0 │ 1 lugar 8
1 0 0 1 │ 1 lugar 9
1 0 1 0 │ 1 lugar 10
1 0 1 1 │ 0 lugar 11
1 1 0 0 │ 0 lugar 12
1 1 0 1 │ 1 lugar 13
1 1 1 0 │ 1 lugar 14
1 1 1 1 │ 1 lugar 15

4) Para cinco variables:

                  CDE 000   001   011   010   110   111   101   100
                AB  ┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
                  00│  1  │  0  │  0  │  1  │  0  │  0  │  0  │  1  │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  01│  1  │  1  │  1  │  0  │  0  │  1  │  1  │  0  │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  11│  0  │  1  │  1  │  1  │  1  │  0  │  1  │  0  │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  10│  1  │  1  │  0  │  1  │  1  │  1  │  1  │  0  │
                    └─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘  


Numeración de los lugares en los MK

                     B  0     1
                   A ┌─────┬─────┐
                   0 │  0  │  1  │
                     ├─────┼─────┤
                   1 │  2  │  3  │
                     └─────┴─────┘


                    BC 00    01    11    10
                   A ┌─────┬─────┬─────┬─────┐
                   0 │  0  │  1  │  3  │  2  │
                     ├─────┼─────┼─────┼─────┤
                   1 │  4  │  5  │  7  │  6  │
                     └─────┴─────┴─────┴─────┘


              CD 00    01    11    10
             AB┌─────┬─────┬─────┬─────┐
             00│  0  │  1  │  3  │  2  │
               ├─────┼─────┼─────┼─────┤
             01│  4  │  5  │  7  │  6  │
               ├─────┼─────┼─────┼─────┤
             11│  12 │  13 │  15 │  14 │
               ├─────┼─────┼─────┼─────┤
             10│  8  │  9  │  11 │  10 │
               └─────┴─────┴─────┴─────┘


                  CDE 000   001   011   010   110   111   101   100
                AB  ┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
                  00│  0  │  1  │  3  │  2  │  6  │  7  │  5  │  4  │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  01│  8  │  9  │  11 │  10 │  14 │  15 │  13 │  12 │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  11│  24 │  25 │  27 │  26 │  30 │  31 │  29 │  28 │
                    ├─────┼─────┼─────┼─────┼─────┼─────┼─────┼─────┤
                  10│  16 │  17 │  19 │  18 │  22 │  23 │  21 │  20 │
                    └─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘





  ¿Cómo realizar estas operaciones de forma sistemática?

  1)  Realizar  agrupaciones  de  1's  con  sus  vecinos  lo  mayor  posible  pero  siempre  en
cantidades potencias de 2.

  2)  No  dejar  ningún  1  sin  agrupar.  Puede  ocurrir  que  un  1  pertenezca  a  más  de  una
agrupación. No se pueden coger agrupaciones dentro de agrupaciones.

  3)  Por  cada  agrupación  de  1's  resulta  un  producto  de  variables.  Cuanto  más  1's  se
agrupen,  más  sencilla  resultará  la  expresión  de  esa  agrupación.  En  MK  de  5  variables,  las
agrupaciones que tomen 1’s de las dos porciones deben ser simétricas respecto al eje central.

  4)  En  cada  agrupación,  cada  una  de  las  variables  puede  aparecer  en  alguno  de  los
siguientes casos:

  a) Si siempre vale 1  -----> Se pone afirmada.
  b) Si siempre vale 0  -----> Se pone negada.
  c) Si cambia de valor (50% de los casos un valor y el otro 50% otro valor)-----> No se pone.

  5) La expresión de  la  función booleana será  la suma  lógica de todos  los productos que
hayan salido.


Definición y Especificación de sistemas combinacionales.

  Un  sistema  combinacional  es  un  circuito  lógico  cuyas  salidas  están  completamente
determinadas en cualquier instante por los valores aplicados a sus variables de entrada.Son circuitos que no tienen bucles de realimentación, es decir una salida no puede usarse como
entrada de una etapa anterior.

  Ejemplo de circuito no combinacional, por tener un bucle de realimentación.
  Ejemplo de circuito combinacional
 Tampoco se pueden unir entre sí dos salidas porque puede darse un conflicto.

Implementación de un sistema combinacional.

  La  implementación  de  un  sistema  es  su  composición  en  unidades más pequeñas. Ejemplo:
Implementar un circuito eléctrico de encendido de una bombilla a partir de una pila, un interruptor y una
bombilla.


Especificación de sistemas combinacionales.

Ejemplo.
  La  especificación  de  un  sistema  combinacional  consiste  en  traducir  el  enunciado  de  un
problema concreto a variables y funciones booleanas cuya tabla de verdad permita encontrar un circuito
lógico que resuelva la situación.

A

B
C
A
B
C
A
B

C
D
¿A·B ó C+D?
Si A=0 y C=1 se produce un conflicto

SISTEMA
COMBINACIONAL

x1
x2
xn
z1
z2
zm  

Especificación de alto nivel.

  La especificación se dice que es de alto nivel cuando se encuentra una tabla de verdad en la que
se  reflejan  los  casos  que  se  pretenden  contemplar  de  manera  similar  al  enunciado  del  problema.
Veamos un ejemplo:

  Una máquina expendedora automática proporciona productos con diversos precios: botella de
agua 0,50 €,  lata de  refresco 1,00 €,   paquete   de galletas 1,50 €   y caja de bombones 2,00 €. Sólo
admite una moneda de 0,50 €, 1,00 € ó 2,00 € para adquirir el producto y sólo devuelve cambio de 1
moneda, caso de que tuviera que devolver cambio. Habrá casos en los que, al no poder proporcionar el
cambio correcto, devolverá la moneda introducida, sin proporcionar el producto.

  Realizar la especificación de alto nivel de la máquina:

  ENTRADAS          SALIDAS

Moneda    Producto pedido         ¿Suministra producto?   Cambio

0,00 €   Botella de agua      No  *    0,00 €
0,00 €   Lata de refresco      No  *    0,00 €
0,00 €   Paquete de galletas      No  *    0,00 €
0,00 €   Caja de bombones      No  *    0,00 €
 
0,50 €   Botella de agua      Sí      0,00 €
0,50 €   Lata de refresco      No  *    0,50 €
0,50 €   Paquete de galletas      No  *    0,50 €
0,50 €   Caja de bombones      No  *    0,50 €

1,00 €   Botella de agua      Sí      0,50 €
1,00 €   Lata de refresco      Sí      0,00 €
1,00 €   Paquete de galletas      No  *    1,00 €
1,00 €   Caja de bombones      No  *    1,00 €

2,00 €   Botella de agua      No  **    2,00 €
2,00 €   Lata de refresco      Sí      1,00 €
2,00 €   Paquete de galletas      Sí      0,50 €
2,00 €   Caja de bombones      Sí      0,00 €


MOTIVO DE LA NEGATIVA
* Dinero insuficiente    ** No hay cambio en una única moneda


Especificación de bajo nivel.

  La especificación se dice que es de bajo nivel cuando los casos posibles se codifican de forma
binaria  a  partir  de  la  especificación  de  alto  nivel.  Veamos  el  mismo  ejemplo  del  apartado  anterior
especificado a bajo nivel. Vamos a codificar los distintos tipos de monedas con 2 bits, y los distintos tipos
de productos también con 2 bits.

  ENTRADAS

  Codif. moneda (m1,m0)    Codificación producto (p1,p0)
  00: Ninguna       00: botella de agua
  01: moneda de 0,50 €    01: lata de refresco
  10: moneda de 1,00 €    10: paquete de galletas
  11: moneda de 2,00 €    11: caja de bombones

  SALIDAS

  Codif. devolución (c1,c0)  Codificación suministro (S)
  00: Ninguna       0: NO da el producto seleccionado
  01: moneda de 0,50 €    1: SI da el producto seleccionado
  10: moneda de 1,00 €
  11: moneda de 2,00 €

  Si "traducimos"  la especificación de alto nivel mediante la codificación citada, queda la tabla de
verdad especificada en bajo nivel, que ya es tratable como funciones y variables booleanas:

  ENTRADAS          SALIDAS

Moneda     Producto pedido        ¿Suministra producto?   Cambio

m1  m0  p1  p0          S    c1  c0

 0   0   0   0          0     0   0
 0   0   0   1          0     0   0
 0   0   1   0          0     0   0
 0   0   1   1          0     0   0

 0   1   0   0          1     0   0
 0   1   0   1          0     0   1
 0   1   1   0          0     0   1
 0   1   1   1          0     0   1

 1   0   0   0          1     0   1
 1   0   0   1          1     0   0
 1   0   1   0          0     1   0
 1   0   1   1          0     1   0

 1   1   0   0          0     1   1
 1   1   0   1          1     1   0
 1   1   1   0          1     0   1
 1   1   1   1          1     0   0


que es la Tabla de Verdad de 3 funciones booleanas (S, c1 y c0) de 4 variables (m1, m0, p1 y p0) cada
una.

 El proceso de diseño de un circuito combinacional consiste en:

1)  Determinar el número de variables de entrada y de salida necesarias,  identificar  las
variables  de  entrada,  asignarles  un  nombre  y  hacer  lo mismo  con  las  variables  de
salida.

  2) Deducir la tabla de verdad que define las relaciones entre las variables de entrada y de
salida.

3) Simplificar las funciones representadas en la tabla de verdad.

  4) Obtener el circuito a partir de las funciones simplificadas.


  Si simplificamos aplicando los mapas de Karnaugh resulta:

0 · 1 · 0 · 1 1 · 0 · 1 1 · 0 · 1 0 · 0 · 1 p p m m p m m p m m p m m S


1 · 0 · 1 1 · 0 · 1 1 p m m p m m c


0 · 1 · 0 0 · 0 · 1 0 · 1 · 1 0 p p m p m m p p m c


cuya implementación resulta sencilla a la vista de estas ecuaciones.  

EJERCICIOS RESUELTOS

1. Representar el mapa de Karnaugh y simplificar la función booleana
4 4
) 15 , 14 , 12 , 7 , 4 ( ) 13 , 6 , 5 ( d m F


    CD
AB

00

01

11

10

00  0  0  0  0

01  X  1  X  1

11  X  1  X  X

10  0  0  0  0



2. Encontrar la tabla de verdad, el mapa de Karnaugh y la expresión booleana más simplificada de una
función booleana de 4  variables que  tome el  valor 1  cuando el número expresado en binario por sus
variables  sea un número primo mayor que 4,  y 0 en el  resto de  los casos. Expresar  la  función como
suma de productos y como producto de sumas.

A  B  C  D  F
0  0  0  0  0
0  0  0  1  0
0  0  1  0  0
0  0  1  1  0
0  1  0  0  0
0  1  0  1  1
0  1  1  0  0
0  1  1  1  1
1  0  0  0  0
1  0  0  1  0
1  0  1  0  0
1  0  1  1  1
1  1  0  0  0
1  1  0  1  1
1  1  1  0  0
1  1  1  1  0


   
   CD
AB

00

01

11

10

00  0  0  0  0

01  0  1  1  0

11  0  1  0  0

10  0  0  1  0

Como suma de productos:
D C B A D B A D C B D C B A F · · · · · · · ) , , , (

Como productos de sumas:
) )·( )·( ·( ) , , , ( C B A C B B A D D C B A F

F = B  


3. Se quiere  implementar un sistema con dos  luces de alarma (diodos LED) y  tres sensores (entradas
digitales).  Llamaremos A  y B  a  las  luces  de alarma,  y  x2,  x1  y  x0 a  los  sensores digitales. El  sistema
deberá funcionar de la siguiente manera:

  * La alarma A se dispara si se recibe señal del sensor x2 exclusivamente.
  * La alarma B se dispara si se recibe señal del sensor x0 exclusivamente.
  * Las dos alarmas se disparan si se recibe señal de al menos dos sensores cualesquiera.

  a) Realizar una especificación tabular del sistema de alarma (tabla de verdad).
  b) Realizar una implementación con puertas AND-OR.
  c) Realizar una implementación con puertas NAND.
  d) Realizar una implementación con puertas NOR.

a)

x2  x1  x0  A  B
 0  0  0  0  0
0  0  1  0  1
0  1  0  0  0
0  1  1  1  1
1  0  0  1  0
1  0  1  1  1
1  1  0  1  1
1  1  1  1  1

b)
0 1 2 x x x A
  c)
0 1 2 x x x A
  d)
2 1 2 0 x x x x A
 
2 1 0 x x x B

2 1 0 x x x B
 
1 0 2 0 x x x x B


4. Se desea diseñar un circuito combinacional que realice el complemento a 2 de un número binario de 4
bits. En el diseño se emplearán puertas OR y XOR. Las salidas de las puertas XOR serán las salidas del
circuito.



b3  b2  b1  b0  b’3  b’2  b’1  b’0  x3  x2  x1  x0
0  0  0  0  0  0  0  0  0  0  0  0
0  0  0  1  1  1  1  1  1  1  1  0
0  0  1  0  1  1  1  0  1  1  0  0
0  0  1  1  1  1  0  1  1  1  1  0
0  1  0  0  1  1  0  0  1  0  0  0
0  1  0  1  1  0  1  1  1  1  1  0
0  1  1  0  1  0  1  0  1  1  0  0
0  1  1  1  1  0  0  1  1  1  1  0
1  0  0  0  1  0  0  0  0  0  0  0
1  0  0  1  0  1  1  1  1  1  1  0
1  0  1  0  0  1  1  0  1  1  0  0
1  0  1  1  0  1  0  1  1  1  1  0
1  1  0  0  0  1  0  0  1  0  0  0
1  1  0  1  0  0  1  1  1  1  1  0
1  1  1  0  0  0  1  0  1  1  0  0
1  1  1  1  0  0  0  1  1  1  1  0
i i i
x b b'
   
0 0 x
 
0 1 b x
 
0 1 2 b b x
 
2 2 0 1 2 3 x b b b b x

b’i
bi
xi

SALIDA DEL CIRCUITO


5. Diseñar un circuito al que se  le  introducen  los 4 bits de un código hexadecimal y cuya salida es  la
excitación  para  activar  un  display  de  7  segmentos,  de  acuerdo  con  la  figura  adjunta.  Los  caracteres
hexadecimales que no son numéricos, deben aparecer en mayúsculas, excepto la "b" y la "d", que deben
aparecer en minúscula. NOTA: Tomar D como el bit más significativo.

               S6
   ╔════════╗         ══════
 D─╢ C   D  ╟─S6        ║      ║
   ║ I   I  ╟─S5      S1║      ║S5
 C─╢ R   S  ╟─S4        ║  S0  ║
   ║ C A E  ╟─S3         ══════    DISPLAY 7 SEGMENTOS
 B─╢ U   Ñ  ╟─S2        ║      ║
   ║ I   A  ╟─S1      S2║      ║S4
 A─╢ T   R  ╟─S0        ║     ║
   ║ O      ║          ══════    
   ╚════════╝           S3
             

a) Escribir la tabla de verdad de todas las funciones booleanas que aparecen.
b) Implementar las funciones de la siguiente forma:

  b1) S1 con puertas AND/OR en dos niveles.
  b2) S2 con puertas OR/AND en dos niveles.
  b3) S4 usando sólo puertas NOR.
  b4) S5 usando sólo puertas NAND.

Hexa  D  C  B  A  S6  S5  S4  S3  S2  S1  S0
0  0  0  0  0  1  1  1  1  1  1  0
1  0  0  0  1  0  1  1  0  0  0  0
2  0  0  1  0  1  1  0  1  1  0  1
3  0  0  1  1  1  1  1  1  0  0  1
4  0  1  0  0  0  1  1  0  0  1  1
5  0  1  0  1  1  0  1  0  1  1  1
6  0  1  1  0  1  0  1  1  1  1  1
7  0  1  1  1  1  1  1  0  0  1  0
8  1  0  0  0  1  1  1  1  1  1  1
9  1  0  0  1  1  1  1  1  0  1  1
A  1  0  1  0  1  1  1  0  1  1  1
b  1  0  1  1  0  0  1  1  1  1  1
C  1  1  0  0  1  0  0  1  1  1  0
d  1  1  0  1  0  1  1  1  1  0  1
E  1  1  1  0  1  0  0  1  1  1  1
F  1  1  1  1  1  0  0  0  1  1  1


D B D C D C B A S · · · · 1


) )·( )·( ( 2 D C B A C B A D B A S


) ( ) ( ) ( 4 D C B A D C A D C B S


) · · ( · ) · · ( · ) · ( · ) · ( 5 D B A D B A C A D C S

Un Poco sobre mi!

Mi nombre es- Isabel Cristina Hernandez Suarez

Estudio Ing. De Sistemas, es decir trato de sobrevivir en la universidad, divirtiendome mientras duré.!
Me encanta el BÉISBOL, Entrenar CROSSFIT, salir de viaje con mi familia, compartir con amigos y trabajar mucho...!. Soy Relativamente disciplinada, pero a su vez tengo carácter fuerte.
Soy una chica muy estudiosa, dedicada, responsable, con metas en la vida, las cuales, quiero cumplirlas, mis principales metas a corto plazo es tratar de ser mejor como persona y desempeñarme con éxito en cada uno de mis días.

CIRCUITOS COMBINACIONALES

Está formado por funciones lógicas elementales (AND, OR, NAND, NOR, etc. ), que tiene un determinado número de entradas y salidas. Es un circuitocuya salida depende solamente de la "combinación" de sus entradas en el momento que se está realizando la medida en la salida. Los circuitos de lógica combinacional son hechos a partir de las compuertas básicas compuerta AND, compuerta OR, compuerta NOT. También pueden ser construidos con compuertas NAND, compuertas NOR, compuerta XOR, que son una combinación de las tres compuertas básicas.

Un circuito combinacional, como su nombre lo sugiere es un circuito cuya salida depende solamente de la “combinación” de sus entradasen el momento que se está realizando la medida en la salida. Analizando el circuito, con compuertas digitales, que se muestra (ver el diagrama) se ve que la salida de cada una de las compuertas que se muestran, depende únicamente de sus entradas.

La salida F (salida final o total del circuito) variará si alguna de las entradas A o B o las dos a la vez cambian. Los circuitos de lógica combinacional son hechos a partir de las compuertas básicas: compuerta AND, compuerta OR, compuerta NOT. También pueden ser construidos con compuertas NAND, compuertas NOR, compuerta XOR, que son una combinación de las tres compuertas básicas.

La operación de los circuitos combinacionales se entienden escribiendo las ecuaciones booleanas y sus respectivas tablas de verdad. Ejemplo de ecuación booleana: F = A.B’+A’.B

Clasificación

Entre los circuitos combinacionales clásicos tenemos:

Lógicos

·         Generador/Detector de paridad

·         Multiplexor y Demultiplexor

·         Codificador y Decodificador

·         Conversor de código

·         Comparador

Aritméticos

·         Sumador

Aritméticos y lógicos

·         Unidad aritmético logica

Éstos circuitos están compuestos únicamente por puertas lógicas interconectadas entre sí.

CIRCUITOS COMBINACIONALES-ANÁLISIS: Se realiza de izquierda a derecha, partiendo de la entrada hasta la salida. Principalmente se tiene en cuenta el retardo de operación. Dependiendo de éste, encontramos dos zonas temporales de operación: estado estacionario y estado transitorio. Transitorio es el tiempo que va desde el cambio de las entradas hasta que la salida se estabiliza (tanto las señales internas como las de salida pueden sufrir cambios). Estacionario es el tiempo que va desde la estabilización del circuito lógico hasta que las entradas vuelven a cambiar (sólo las señales de entrada pueden sufrir algún cambio).

Tipos de Circuitos Combinacionales

Hay varios tipos de circuitos combinacionales, atendiendo a su “densidad de integración”; esto es, a su número de transistores o de puertas lógicas. Circuitos SSI: Son circuitos de baja escala de integración, y contienen hasta 10 puertas lógicas o 100 transistores. Circuitos MSI: Son los de media escala de integración, y contienen entre 10 y 100 puertas lógicas, o de 100 a 1.000 transistores. Circuitos LSI: Son circuitos de alta escala de integración, y tienen entre 100 y 1.000 puertas lógicas, o de 1.000 a 10.000 transistores. Circuitos VLSI: Son los de más alta escala de integración, y tienen más de 1.000 puertas lógicas o más de 10.000 transistores.

• Los circuitos MSI se clasifican de la siguiente forma según la función que desempeñan en los sistemas digitales;

•  DE COMUNICACIÓN: Transmiten y modifican información. Codificadores: Con prioridad o sin prioridad. Decodificadores: Excitadores y no excitadores. Multiplexores y demultiplexores. 

• ARITMÉTICOS: Operan con los datos binarios que procesan. Sumadores y semisumadores. Comparadores. Restadores

• CODIFICADOR: Es un dispositivo que transforma una señal expresada en un código humano a un código binario. Se denomina completo si las entradas son 2N, e incompleto si éstas son menores que 2N. El codificador con prioridad es capaz de atender a varias entradas simultáneas y determinar el criterio que da prioridad a una señal u otra, mientras que el sin prioridad solo acepta una entrada cada vez

• DECODIFICADOR podría definirse como la función inversa del anterior. Dispone de n entradas y 2n salidas. Atendiendo a su salida, el decodificador puede ser activo a nivel alto (‘1’) o a nivel bajo (‘0’) La mayoría integran un dispositivo de control mediante una entrada Enable, (que puede ser activa a niveles alto o bajo) tal que si no se da, el decodificador no se activa. También puede requerirse una combinación de ellos, a modo de clave. También existen decodificadores para los que a partir de las diferentes entradas posibles se active más de una salida. Estos son los llamados ‘decodificadores-es.

Funciones Lógicas y Circuitos Combinacionales

1. Compuertas Lógicas

El número total de posibles combinaciones de entradas binarias es determinada con la siguiente fórmula:  N = 2n

Invertidor (NOT)

Ejecuta la función lógica básica llamada inversión o complementación.  Su propósito es cambiar de un nivel lógico a su nivel opuesto.  En término de bits, cambia de 1 a 0 y de 0 a 1.

AND

Ejecuta la multiplicación lógica, comúnmente llamada la función AND.  La salida sólo es HIGH (1) cuando todas las entradas son HIGH (1), de lo contrario la salida es LOW (0).

OR

Ejecuta la suma lógica, comúnmente llamada la función OR.  La salida es HIGH (1) si al menos una entrada es HIGH (1), de lo contrario es la salida es LOW (0).

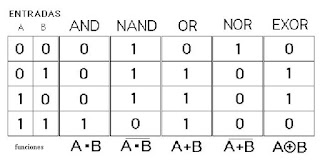
NAND

Es un elemento lógico muy popular porque se puede utilizar como una función universal.  La salida sólo es LOW (0) cuando todas las entradas son HIGH (1), de lo contrario la salida es HIGH (1).

NOR

Al igual que el NAND, es de gran utilidad por su propiedad universal.  La salida es LOW (0) si al menos hay una entrada HIGH (1).

XOR

Tiene sólo dos entradas.  La salida es HIGH (1) sólo cuando las entradas tienen niveles opuestos, de lo contrario (entrada del mismo nivel) la salida es LOW (0).

XNOR

Tiene sólo dos entradas.  La salida es LOW (0) sólo cuando las entradas tienen niveles opuestos, de lo contrario (entrada del mismo nivel) la salida es HIGH (1).

Exor

Esta puerta lógica , la EXOR, nos da a la salida un 0 siempre que sus entradas tengan igual valor . En el resto de los casos da 1 a la salida.