CIRCUITOS SECUENCIALES

INTRODUCCIÓN

Los sistemas digitales que introducen la dependencia temporal son conocidos como sistemas secuenciales. Una definición más rigurosa de sistema secuencial puede ser la siguiente: Un circuito de conmutación secuencial se define como un circuito bivaluado en el cual, la salida en cualquier instante depende de las entradas en dicho instante y de la historia pasada (o secuencia) de entradas.

CARACTERÍSTICAS

• Poseen uno o más caminos de re-alimentación, es decir, una o más señales internas o de salida se vuelven a introducir como señales de entradas. Gracias a esta característica se garantiza la dependencia de la operación con la secuencia anterior. 

• Como es lógico, existe una dependencia explícita del tiempo. Esta dependencia se produce en los lazos de re-alimentación antes mencionados. En estos lazos es necesario distinguir entre las salidas y las entradas re-alimentadas.

ELEMENTOS

• Elementos de retraso, ya sean explícitos o implícitos debido al retraso de la lógica combinacional. Este retraso es fijo e independiente de cualquier señal.

 • Elementos de memoria, que son dispositivos que almacena el valor de la entrada en un instante determinado por una señal externa y lo mantiene hasta que dicha señal ordene el almacenamiento de un nuevo valor. La diferencia de comportamiento entre ambos elementos radica en que la salida del elemento de retraso es una copia de la señal de entrada; mientras que el elemento de memoria copia determinados instantes de la entrada (determinados por una señal externa), y no la señal completa, el resto del tiempo la salida no cambia de valor

Circuitos Lógicos Secuenciales

Los bloques básicos para construirlos son los circuitos flip-flops.  Los circuitos lógicos secuenciales son extremadamente importantes debido a su característica de memoria.

Los flip-flops también se denominan "cerrojos", "multivibradores biestables" o "binarios".  Los flip-flops pueden construirse a partir de puertas lógicas, como, por ejemplo, puertas NAND, o comprarse en forma de circuitos integrados.  Los flip-flops se interceptaran para formar circuitos lógicos secuenciales que almacenen datos, generen tiempos, cuenten y sigan secuencias.

Funcionalidad

El circuito secuencial debe ser capaz de mantener su estado durante algún tiempo, para ello se hace necesario el uso de dispositivos de memoria. Los dispositivos de memoria utilizados en circuitos secuenciales pueden ser tan sencillos como un simple retardador (inclusive, se puede usar el retardo natural asociado a las compuertas lógicas) o tan complejos como un circuito completo de memoria denominado multivibrador biestable o Flip Flop

FLIP-FLOP D

Tiene solamente una entrada de datos (D) y una entrada de reloj (CK).  El flip-flop D, con frecuencia, se denomina flip-flop de retardo (y de datos).  Este nombre describe con precisión la operación que realiza.  Cualquier que sea el dato en la entrada (D), éste aparece en la salida normal retardado un pulso de reloj.  El dato es transferido a la salida durante la transición del nivel BAJO al ALTO del pulso de reloj.

Otros nombres usados para este tipo de circuitos son: MultiVibradores, Basculas, Bies-tables

Los Flip-Flops son las unidades básicas de todos los sistemas secuenciales. Existen cuatro tipos: el RS, el JK, el T y el D. Y los últimos tres se implementan del primero.


Son capaces de permanecer en un estado determinado durante un tiempo indefinido. Esta característica es amplia mente utilizada para memorizar información.



El Flip Flop SR (Set/ Reset), abreviadamente FF-SR

El FF-SR es un dispositivo con dos entradas (Set y Reset) y una variable de estado o salida (Q) capaz de guardar un bit de información y funciona como sigue:

Si la entrada Set pasa a 1 la salida Q pasa 1
Si la entrada Reset pasa a 1 la salida Q pasa a 0
Si ni Set ni Reset cambian la salida Q no cambia
Set y Reset no pueden cambiar simultáneamente.






FLIP-FLOP JK

Este dispositivo puede considerarse como el flip-flop universal; los demás tipos pueden construirse a partir de él.





Tabla de Funcionamiento

La tabla de funcionamiento de este circuito es parecida a la de un combinacional pero en la cual se ha introducido la información "tiempo" que en el caso de circuitos secuenciales se vuelve esencial.

Entradas en tn Salida en tn+1
S R Q+

0 0 Q0
0 1 0
1 0 1
1 1 no valida

En donde se ha utilizado la siguiente notación:

tn = instante en el cual se aplican las entradas.

tn+1 = instante siguiente, cuando el circuito proporciona su salid

Q0 = salida Q en el instante tn

Q+ = salida en el instante tn+1

Aplicaciones de los Flip-Flop

Todos estos tipos de Flip-Flops se emplean para construir módulos funcionales que realizan tareas de mas alto nivel, algunas de las cuales describir a continuación.

Contadores

Permiten llevar la cuenta del número de veces que se repite un suceso. Para ello memorizan la cuenta actual y la incrementan cada vez que el evento vuelve a ocurrir. Como elemento de memoria se usa algún tipo de Flip-Flop, tantos como sea precisos para memorizar la cantidad máxima que este previsto contar.





Clasificación de los Sistemas Secuenciales

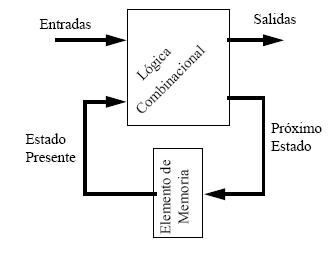
Uno de los primeros problemas de los circuitos secuenciales era determinar el momento en el que el próximo estado debía pasar a estado presente, sin capturar situaciones no deseadas como pueden ser los azares. Este problema es lo que se conoce como sincronizar, cuyas soluciones dieron lugar a una de la principales clasificaciones de los sistemas secuenciales. Así podemos dividir los sistemas en dos categorías: Lógica Combinacional Elemento de Memoria Entradas Salidas Próximo Estado Presente Estado Figura 1.3.- Modelo clásico de un sistema secuencial.

• Sistemas asíncronos.- La sincronización depende exclusivamente de los retrasos de la lógica combinacional, sin necesidad de ninguna señal externa al sistema.

• Sistemas síncronos.- La sincronización depende exclusivamente de una señal externa al sistema, conocida generalmente como señal de reloj. Esta señal de reloj controlará el comportamiento de los elementos de memoria

Las operaciones de un sistema asíncrono tienen efecto, es decir, se almacena el próximo estado, en intervalos temporales diferentes. Por lo tanto, su velocidad de operación será distinta para cada secuencia de entradas. De esta forma se toma como el parámetro de la velocidad de operación el valor medio de todas las velocidades. Así, la operación de un sistema asíncrono se denomina operación del caso medio. 

En cambio, las operaciones de un sistema síncrono tienen efecto en el mismo intervalo temporal, el dictaminado por el periodo de la señal de reloj. Por lo tanto, su velocidad de operación será siempre la misma para todas las secuencias de entrada. Esta velocidad debe ser tal que todas las operaciones tengan el tiempo necesario para poder llevarse a cabo. Así, la velocidad de un sistema síncrono (y por tanto la frecuencia de la señal de reloj asociada) debe estar limitada por la operación más lenta. A este tipo de operaciones se le suele denominar operación del caso peor.

Ejemplo de diseño de un contador

Se desea un contador que solo pueda contar 0, 1, 2, 3 y 4. A un contador as se le denomina contador módulo 5 pues, no importa cuantas veces ocurra el suceso el conteo ser 0, 1, 2, 3 4, lo cual corresponde al resto de dividir el conteo real por 5 (por ejemplo, si el suceso se ha repetido 7 veces, el contador haber entregado los conteos 1, 2, 3, 4, 0, 1, 2 siendo el ultimo valor entregado 2, que es el resto de dividir 7 por 5)

Est claro que los estados diferentes que podr tener el sistema secuencial buscado sern cinco. Adems, las transiciones entre estados estn tambin muy claras: del estado 0 slo se puede pasar al 1, del 1 al 2, del 2 al 3, del 3 al 4, y por ltimo de 4 al 0. No habiendo posibilidad de otras transiciones entre estados. La nica entrada del sistema es la seal a contar E.

Con esto en mente podemos construir la tabla siguiente:

Entrada ESuceso a contar	Estado Actual			Estado Siguiente			Flip Flop 2		Flip Flop 1		Flip Flop 0
	Q2	Q1	Q0	Q2+	Q1+	Qo+	J2	K2	J1	K1	J0	K0
pasa de 0 a 1	0	0	0	0	0	1	0	X	0	X	1	X
pasa de 0 a 1	0	0	1	0	1	0	0	X	1	X	X	1
pasa de 0 a 1	0	1	0	0	1	1	0	X	X	0	1	X
pasa de 0 a 1	0	1	1	1	0	0	1	X	X	1	X	1
pasa de 0 a 1	1	0	0	0	0	0	X	1	0	X	0	X

A partir de esta tabla se pueden encontrar fcilmente las relaciones entre el estado actual o de partida, y las entradas de los Flip Flop:

Representación de los sistemas secuenciales.

 De igual forma que existe una representación de los sistemas combinacionales (mediante tablas de combinaciones), los sistemas secuenciales también tienen sus formas de representación. Éstas son algo más complejas, debido a la dependencia temporal. Así, podemos encontrar las siguientes formas equivalentes.

 • Diagrama de estados, es un grafo orientado en el que cada nudo es un estado y cada transición indica el cambio, tanto de estado como de salida, respecto a un cambio en alguna de las señales de entradas.

 • Tablas de estado y de salida, es una representación tabular del grafo anterior. Las entradas se representan como columnas, y los estados presentes como filas; y en el interior de cada celda, se indica el próximo estado y el valor que tomará la salida cuando sufra la transición.

Los computadores son implementaciones de lógica Booleana:

. • Las funciones Booleanas se describen completamente por medio de tablas de verdad.

 • Las compuertas lógicas son pequeños circuitos eléctricos que implementan operadores lógicos. 

• Los computadores consisten de circuitos lógicos combinacionales y secuenciales

 • Los circuitos combinacionales producen salidas inmediatamente después de que sus entradas cambian.

 • Los circuitos secuenciales requieren de las señal de reloj para producir cambios en las salidas 

• Los circuitos secuenciales básicos son los flip flops. 

• El comportamiento de los circuitos secuenciales puede ser expresado utilizando tablas de comportamiento.

En todo CIRCUITO SECUENCIAL nos encontraremos con:

a) Un conjunto finito, n, de variables de entrada (X1, X2,..., Xn).

b) Un conjunto finito, m, de estados internos, de aquí que los estados secuenciales también sean denominados AUTÓMATAS FINITOS. Estos estados proporcionarán m variables internas (Y1,Y2,..., Ym).

c) Un conjunto finito, p, de funciones de salida (Z1, Z2,..., Zp).

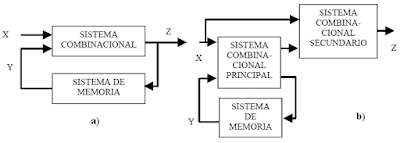
Dependiendo de como se obtengan las funciones de salida, Z, los sistemas secuenciales pueden tener dos estructuras como las que se observan en la siguiente figura, denominadas:

a) Máquina de Moore.

b) Máquina de Mealy.

SIMBOLOGIA

FIGURA.1

FIGURA.2

CONTADOR